角平分线成比例定理是数学中的一种定理,该定理指出三角形内角平分线所对边所得的两条线段和这个角的两边对应成比例。三角形的三条角平分线相交于一点,并且这一点到三条边的距离相等。

证明
如图,已知:在△ABC中,AD是∠BAC的角平分线
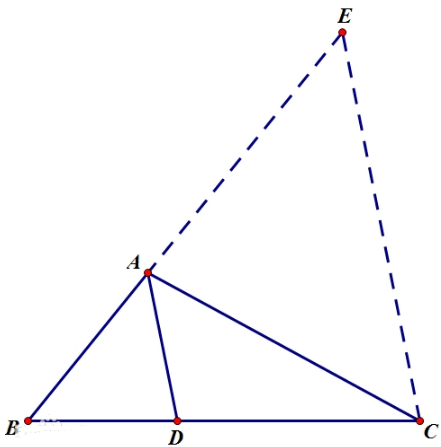
求证:AB/AC=BD/CD
证明:作CE∥AD交BA延长线于E。
∵CE∥AD
∴AB/AE=BD/CD(平行线分线段成比例)
∵CE∥AD
∴∠BAD=∠E,∠CAD=∠ACE
∵AD平分∠BAC
∴∠BAD=∠CAD
∴ ∠ACE=∠E
∴ AE=AC
又∵AB/AE=BD/CD
∴AB/AC=BD/CD
